Художественные средства композиции

Высокие художественные достоинства мебели - целостность формы, композиционное единство элементов, образная выразительность - достигаются художником-конструктором в процессе работы над формой с использованием всего арсенала художественных средств композиции, основными из которых являются отношения и пропорции, ритм и масштабность, единство и соподчинение, тектоника, нюанс и контраст, цветовая гармония и др. Композиционные средства в работе над формой должны использоваться не формально, а в тесной связи с функцией изделия, его конструктивной схемой, технологией изготовления, с учетом пространственных и масштабных связей человек - мебель - среда.

Отношения и пропорции могут быть простыми (арифметическими), основанными на целостных соотношениях величин, и иррациональными (геометрическими).

Примеры простых отношений в измерениях - модульные системы, в которых размеры изделий и их элементов устанавливаются кратными единой расчетной величине - модулю, являющемуся мерой всех элементов конструкций; отношения сторон в квадрате - 1:1; в египетском треугольнике 5:4:3 и др.

В основе иррациональных отношений лежат геометрические построения, основанные на несоизмеримом (иррациональном) соотношении величин.

Большинство форм мебели, как уже отмечалось, можно представить в виде простых геометрических фигур, а отношения элементов изделий свести к отношениям сторон прямоугольников.

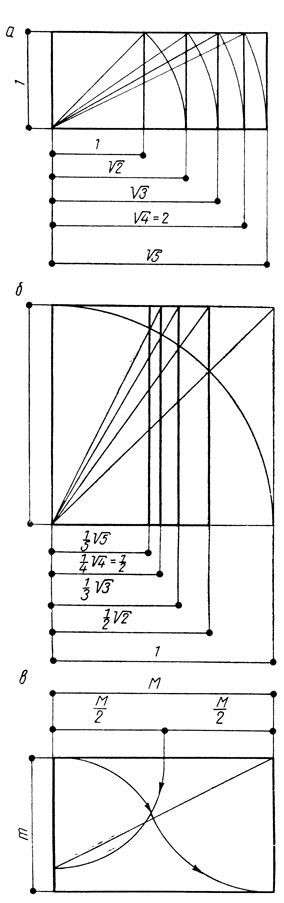
Рис. 28. Графическое построение прямоугольников из корня величин: а - прямой; б - обратной; в - с отношением сторон в 'золотом сечении'

Квадрат, являющийся частным случаем как в арифметических, так и в геометрических отношениях, может служить отправной фигурой и при изучении геометрических построений. Так, сторона прямоугольника, построенного на диагонали исходного квадрата, равна √2. Такой прямоугольник называется прямоугольником √2. Прямоугольник, построенный на диагонали прямоугольника √2, одна сторона которого равна 1, а другая √3, называется прямоугольником √3. Дальнейшие аналогичные построения дают множество прямоугольников из корня прямой величины с отношениями сторон 1:√5; 1:√7 и т. д. (рис. 28, а).

Если в качестве исходной единицы принята длинная сторона, а короткая сторона прямоугольника соответственно уменьшается, можно получить группу прямоугольников обратной величины, подобных рассмотренным выше. Алгебраически это может быть выражено уравнением

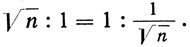
Графическое построение прямоугольников корней из ¹/₂; ¹/₃; ¹/₅ изображено на рис. 28, б.

Прямоугольники √4 и 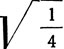являются в то же время и арифметическими, так как они могут быть построены в первом случае складыванием двух квадратов, а во втором - непосредственным делением квадрата на два равных между собой прямоугольника.

Прямоугольники корней прямой и обратной величины, полученные путем геометрического построения, называются основными. Дополнительными прямоугольниками являются такие, которые при добавлении к исходным образуют с ними квадрат.

Прямые, обратные и дополнительные прямоугольники дают возможность получить разнообразные поверхности предельной сложности путем их деления или комбинирования.

Большое распространение в практике пропорционирования получил метод построения сложных прямоугольников в отношении "золотого сечения". В основе метода лежит деление отрезка прямой на две части, причем больший отрезок А так относится к меньшему Б, как сумма А+Б к большему, т. е.

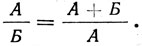
Характерной особенностью "золотого сечения" является то, что сумма двух величин относится к большей величине также в отношении "золотого сечения", т. е. величина, расчлененная в отношении "золотого сечения", сама как целое вступает во взаимодействие со своими частями.

Выражение золотого сечения можно получить, обозначив длину всего отрезка через а, а большую его часть через X, т. е.

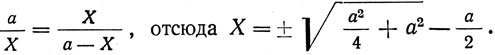
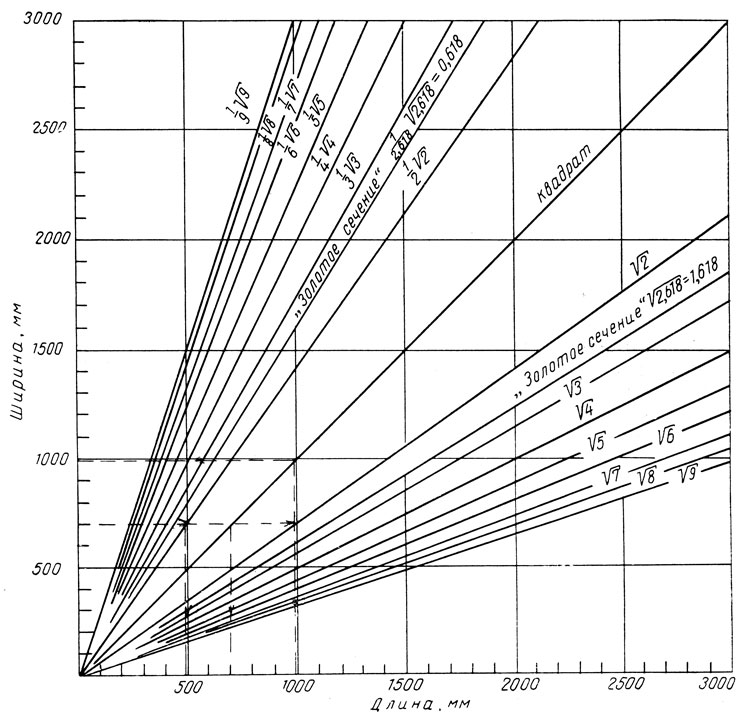
Рис. 29. Диаграмма, позволяющая определить пропорциональные размеры основных и дополнительных прямоугольников корней прямой и обратной величины и 'золотое сечение'. Порядок определения размеров прямоугольников в отношении 1:√2 и 1:^√2/₂ показаны на диаграмме стрелками

Если принять а= 1, то Х = 0,618. Это и есть численное выражение коэффициента золотого сечения. Эта величина определяется как предел отношения между двумя последовательными членами ряда 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144..., который может быть продолжен до бесконечности, так как каждый член его равен сумме двух предыдущих. Графическое построение прямоугольника с отношениями сторон в "золотом сечении" изображено на рис. 28, в и 29.

В работе художника-конструктора над формой мебели появляется необходимость членения поверхностей, что может быть выполнено с использованием изложенных выше методов.

Так, основные прямоугольники делятся при помощи обратных в соответствии с уравнением

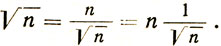
Если n целое число, получается ряд: 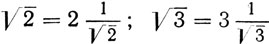и т. д., т. е. прямоугольник корня из n может быть разделен на п равных прямоугольников корня ¹/_n.

Рассмотренные двухмерные отношения еще не обеспечивают единства всех элементов формы. Художник-конструктор должен стремиться обеспечить последовательную закономерность отношений между элементами формы, между элементами и формой, т. е. пропорциональность между частным и целым.

Попытка использовать какие-либо определенные отношения и пропорции может привести к неудовлетворительному, формальному решению, если пренебречь другими факторами, связанными со свойством геометрической формы. К категорическим рекомендациям по выбору отношений и пропорций следует относиться осторожно.

Не менее важным средством, обеспечивающим целостность построения и восприятия композиции и гармонического единства между частями, является ритм. Ритм представляет собой закономерное чередование или повторение форм и интервалов между ними. Простейшей закономерностью подобного рода является повторение равных форм без интервалов (рис. 30, а) или равных форм при равных интервалах (рис. 30,6). В первом случае элементами, членящими форму, служат границы формы. Такой порядок расположения элементов в пределах формы называется простым метрическим рядом. Метрический ряд, образованный сочетанием двух или более простых рядов, называется сложным. Сложные ряды образуются чередованием различных форм при равных интервалах, равных форм при неравных интервалах (рис. 30, в) и неравных форм при неравных интервалах.

Ритмический порядок образуется последовательным закономерным возрастанием или убыванием элементов форм или интервалов между ними (рис. 31, а б) в арифметической или геометрической прогрессии. Сложные ритмические ряды образуются сочетанием простых или сложных метрических рядов, сочетанием метрических и ритмических рядов (рис. 31, в), сочетанием ритмических рядов.

Рис. 30. Примеры метрических рядов: а - метрический ряд, образованный группой ящиков без интервала; б - метрический ряд в спинке дивана и стула, образованный равными формами при равных интервалах; в - метрический ряд в спинке кресла-качалки, образованный равными формами при неравных интервалах

Метрический и ритмический порядок может быть применим не только к геометрическому построению формы, ее размерам и интервалам, но и к цвету, фактуре, текстуре древесины. Степень сложности ритмических построений определяется композиционными задачами и может изменяться в значительных пределах, как по вертикали, так и по горизонтали, обеспечивая единство элементов формы, подчеркивая ее статику или динамику, характер соподчиненности элементов, выявляя центр композиции и т. д.

Единство и соподчинение - важнейшие закономерности композиции, обеспечивающие целостность восприятия формы. При формообразовании выявляются главные и подчиненные элементы композиции путем четкого разграничения процесса по функциональной значимости. Внешними признаками главного элемента по отношению к подчиненному являются большая величина, простота формы, положение относительно осей симметрии и т. д. При симметричном характере композиции главная часть располагается центрально, а подчиненные по обе ее стороны равномерно повторяют друг друга. При этом ось симметрии является одновременно и осью равновесия. При неравномерном развитии подчиненных частей по отношению к главной части композиция будет асимметричной. В этом случае для достижения единства необходимо зрительно уравновесить все части композиции, что достигается соответствующим расположением оси равновесия и другими композиционными приемами (масштабностью, ритмом, цветом и др.). В сложных композициях симметричные группы элементов часто сочетаются с асимметричными, увеличивая общую художественную выразительность.

Рис. 31. Примеры ритмических рядов: а - ритмические ряды, образованные группами ящиков стола без интервала; б - ритмический ряд, образованный закономерным изменением формы поперечного бруска спинки стула и интервала между ними; в - сочетание ритмических и метрических рядов, образованных элементами заполнения стеллажа

Активные средства композиции, усиливающие эмоциональное воздействие изделий,- тождество, нюанс и контраст. Понятие тождество характеризует равенство элементов. Нюанс предполагает незначительное отличие или оттенок, а контраст - резко выраженное различие по форме, размерам, цвету или другим свойствам сравниваемых объектов.

Масштабность определяет степень соответствия размеров рассматриваемой формы или ее элементов размерам человека, назначению изделия и окружающему пространству. Изделия и элементы мебели могут быть соразмерны телу человека, интерьеру, друг другу. Художник - конструктор в процессе работы над формой стремится к установлению строгого соответствия масштабов проектируемого изделия относительно человека и окружающей его материальной среды или в зависимости от общего композиционного замысла путем рационального преувеличения или приуменьшения некоторых привычных человеку размеров обеспечить торжественность, величие и монументальность восприятия окружающего пространства.

Форма и конструкция. Характеризуя требования, предъявляемые к современной мебели, мы установили основные задачи, решаемые художником-конструктором на стадии функционального анализа и направленные на создание необходимого комплекса эксплуатационных удобств. Решение этих задач тесно связано с поиском эстетически целесообразной формы и конструктивной схемы, обеспечивающей надежную работу изделия. Одним из важнейших вопросов в этой связи является тектоника конструкции, под которой понимается выявление и использование в художественных целях конструктивных особенностей изделий. При этом элементы формы преобразуются в единую систему, выявляющую главные художественные особенности конструкции, характер ее работы, соотношения масс, распределение нагрузок, несущие и несомые элементы и т. д.

Рис. 32. Форма опоры консольного стола хорошо передает работу конструкции. Сечения деталей увеличены в местах действия максимального изгибающего момента. Конструкция кажется легкой и динамичной

Конструктивная выразительность формы особо проявляется в изделиях мебели с открытой пространственной структурой, в которых тектоническая основа конструкции может быть выражена наиболее четко. Форма воспринимается наблюдателем как работающая конструктивная схема, через отдельные элементы конструкции, т. е. форма как бы отождествляется с конструкцией. В этом случае рациональное конструктивное решение определяет эстетическое совершенство форм (рис. 32 и 33).

Рис. 33. Неоправданное усложнение опоры кресла вызывает затруднения в оценке работы конструкции

В изделиях с объемной формой связь с конструктивной схемой проявляется менее четко. Однако и здесь есть определенная зависимость между конструкцией изделия и внешней формой. Объемные формы мебели так же разнообразны, как и пространственные, начиная со строгих форм, ограниченных плоскостями, кончая сложными пластическими - "скульптурными".

В том и другом случае задача художника - конструктора состоит в обеспечении максимального соответствия формы функциональному назначению предмета, конструкции изделия и материалу. Художник- конструктор стремится убрать все лишнее, не связанное с конструкцией и функцией изделия, обеспечивая чистоту восприятия формы.

САПЕМ-ИНВЕСТ вот тут.